###Old Time Mathematics
The latest acquisition is a brand new, never opened Sterling brand
10" Senior Mannheim sliderule. The date on the sticker is 1972, so
it has been sitting unused for 47 years. American plastic at its
best. The history page for the [Oughtred
Society](
http://www.oughtred.org/history.shtml) summarizes the
history of the slide rule:
>The slide rule has a long and distinguished ancestry … from William
>Oughtred in 1622 to the Apollo missions to the moon ... a span of
>three and a half centuries … it was used to perform design
>calculations for virtually all the major structures built on this
>earth during that long period of our history … an amazing legacy
>for something so mechanically simple.
As I may have mentioned previously, the last slide rules were
probably manufactured around 1976, about the time I went into high
school. Electronic calculators were still a bit pricey, but those
students that did have them were prohibited from using them in math
classes. So our group fell between the cracks as we were left with
pencil and paper. For our current times the question is, what is
the need of using such a device when even a simple calculator is
available at the local dollar store?
- It's a great aid in maintaining math skills as well as [an
intuition for numerical relationships and
scale](
https://en.wikipedia.org/wiki/Slide_rule#Compared_to_electronic_digital_calculators)
that would otherwise be lost by relying on electronic calculators.
- As it does not consume any power, no batteries required.
- Does not require a software security update every week.
- It is not affected by "planned obsolescence." Whether it is truly
obsolete is arguable.
- Will last decades if not hundreds of years particularly if it is
good old American plastic.
- No need to worry about spyware, malware, tracking or snooping.
I could go on and on, but I think the idea has been conveyed. The
caveat is that there is a certain learning curve and of course some
practice is required, but there is a certain sense of achievement
when certain real world problems are solved using nothing but a
pencil, paper and slide rule. If it was used to build bridges and
get us to the moon, most likely it will take care of my calculating
needs. I will not get into the "how to's" of the slide rule as
there is a wealth of information on the net on the operation of this
device. I would recommend a nice series of
[videos](
https://www.youtube.com/playlist?list=PL_qcL_RF-ZyvJYtIr9NRXJX958d6BgdbN)
by Professor Herning that sheds a clear light on the basic use and
theory of the slide rule. Let us, however look at a real world
problem that also involves dealing with the placement of the decimal
point when calculating with a slide rule:

This one is a common problem I encounter here in the sticks whether
it is determining head required for a well pump to getting the
height of one of the Redwoods or Douglas Fir on the property etc.
There are some people who could figure this one out in their heads,
I am not one of them, so let use resort to the slide rule and see
what we get.
We know angle A is 40° and we know the length of b is 6, so what
is the height of our imaginary tree? Having forgotten most of my
basic high school trig, I located on the net, a nice table for
solutions of right triangles. When we know angle A, and distance b
then b * (Tangent A) will give us our height or in this case the
distance of B to C. On this particular slide rule, removing the
slide, flipping it over, and reinserting, we can get the S, L, and T
scales.

After lining up the indexes, we move the hairline over to 40° on
the T scale, we read the result directly below on the D scale.

The answer is 84, but since on the tangent scale, the significant
digits are always to the right of the decimal point, the answer in
this case is .84. So now we are left with b * .84 = height. Let's
pop the slide out again, flip it over and put it back in to get the
C scale which we will use for multiplication.
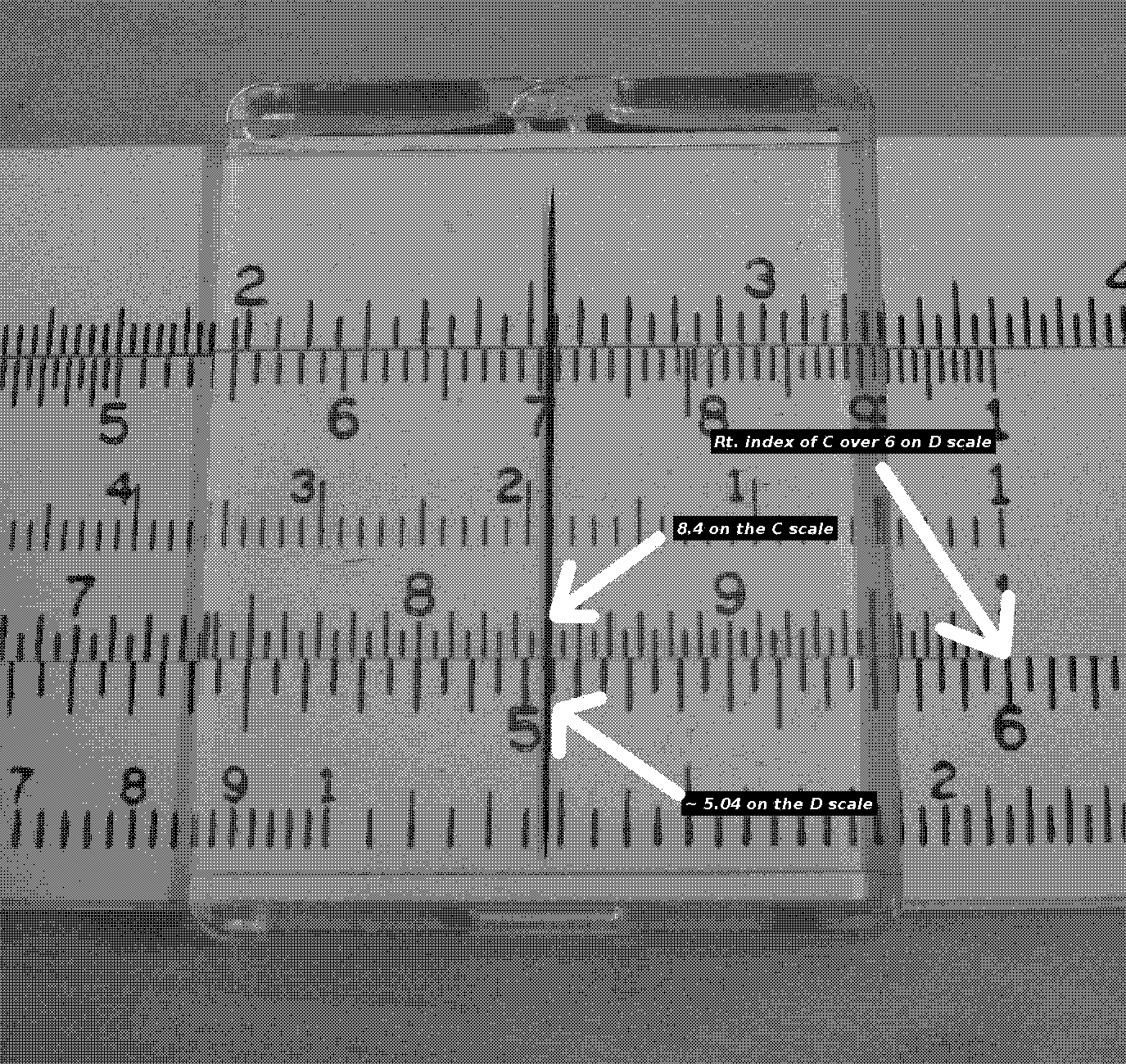
Now the major reason many people shy away from the slide rule is it
does not place the decimal point for you. There are various and
sundry methods to correctly place the decimal point, but the one
that has worked for me thus far is converting the numbers to
scientific notation and then performing the required calculations on
the slide rule. The goal is to shift the decimal point to where we
have a single nonzero digit to the left of the decimal. In this
case, b (6) converts to 6 E0 (like on a cheap calculator). E simply
means "exponent of ten" or "times ten to the power of." For the
second value, we move the decimal to the right 1 place which gives
us 8.4 E-1. So now we have 6 E0 * 8.4 E-1. Now we slide the right
side C index over the 6 on the D scale then move the hairline over
8.4 on the C scale. The answer is directly below on the D scale
which in this case is about 5.04. Since we are multiplying, we
simply add the exponents (0 + (-1) = -1), but since the product of
coefficients is greater than 10 (a change in magnitude since 6 * 8.4
is 10 or more), we have to add 1 to our exponents (0 + (-1) + 1)
which gives us E0 so no need to move the decimal. Our answer is
approx. 5.04 (approximate since the best we can generally get is a
result of up to 3 significant figures on a 10" slide rule which more
than good enough for most applications). Let's have a look at what
the calculator does:

Pretty darned close, but for just about any purpose, it is spot on.
Tags: computing, hand-tools, data-security, retro